寻找两个有序数组的中位数

问题描述

给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。

请你找出这两个有序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。

你可以假设 nums1 和 nums2 不会同时为空。

示例1:

nums1 = [1, 3]
nums2 = [2]

则中位数是 2.0

示例2:

nums1 = [1, 2]
nums2 = [3, 4]

则中位数是 (2 + 3)/2 = 2.5

这里只讨论算法的时间复杂度为 O(log(m + n))的解法，暴力解法的时间复杂度为O(m+n)，这里不讨论。

解题思路一

看到log，自然而然的就会想到二分法解决问题，题目要求是求解中位数，其实就是求解第k小的数，而这个k取决与m和n的值，如果m+n为奇数，那么毫无疑问这个k就是int((m+n)/2),如果是偶数呢，那么k就是int((m+n)/2)再加上它后面的那个数再乘0.5（这里是乘0.5而不是除2，是因为除2还需要声明一个浮点数，简化代码）。
对于求第k小的数，有特殊的解法。由于两个数组是有序的，所以说如果我们要找第k小的数，只需要分别找到两个数组中前k/2的数，然后比较他们的最大值，这样就可以直接排除k/2个数，这样说可能很多人还是云里雾里听不懂，我们来看如下一个例子：
假设我们要找第七小的数字：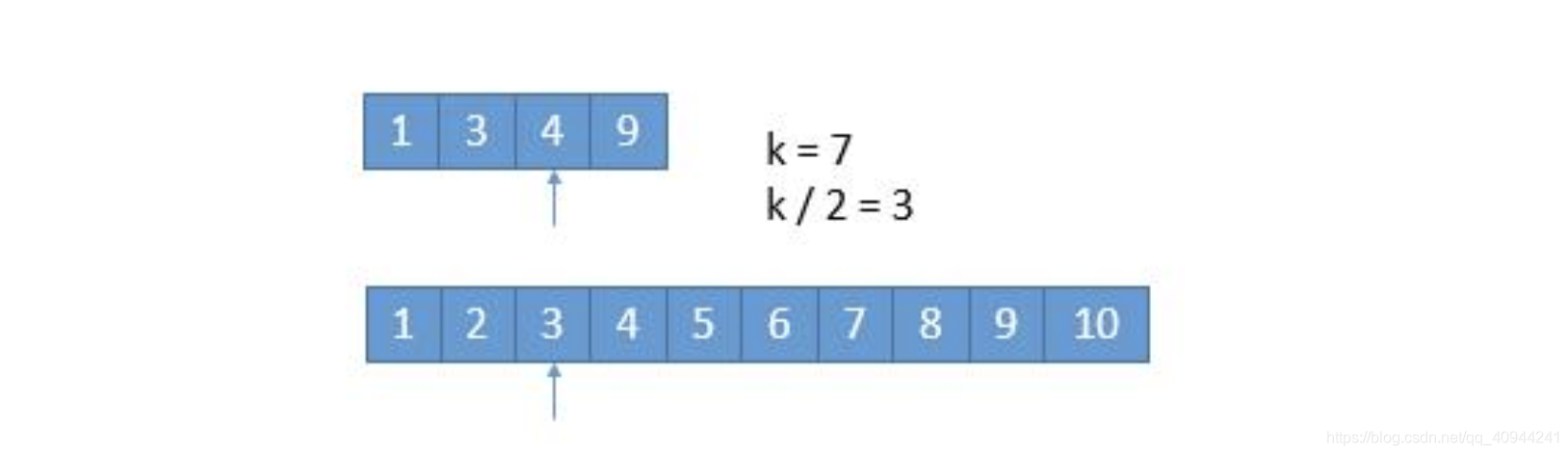

我们比较两个数组的第k/2个数（如果k是奇数就除以二，向下取整，所以这里是3），上方数组的4和下面数组的3做比较，4>3，所以我们可以确定下面数组的前k/2的数都不是第k小的数，所以都可以排除。
橙色部分表示已经被去掉的数字：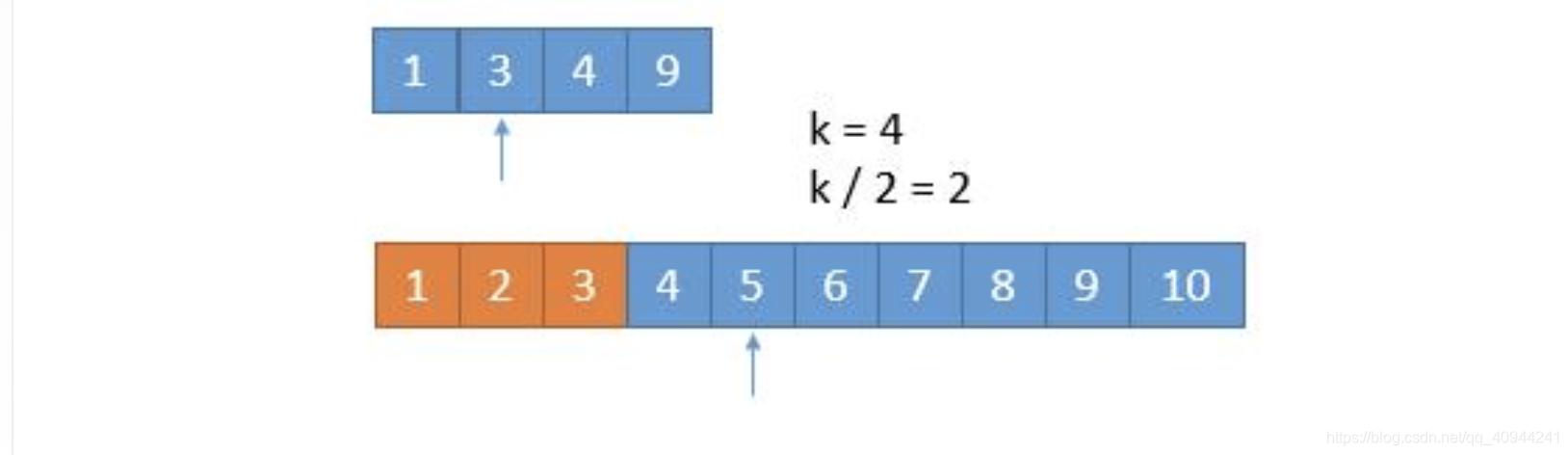

由于我们已经排除掉了 3 个数字，就是这 3 个数字一定在最前边，所以在两个新数组中，我们只需要找第 7 - 3 = 4 小的数字就可以了，也就是 k = 4。此时两个数组，比较第 2 个数字，3 < 5，所以我们可以把小的那个数组中的 1 ，3 排除掉了。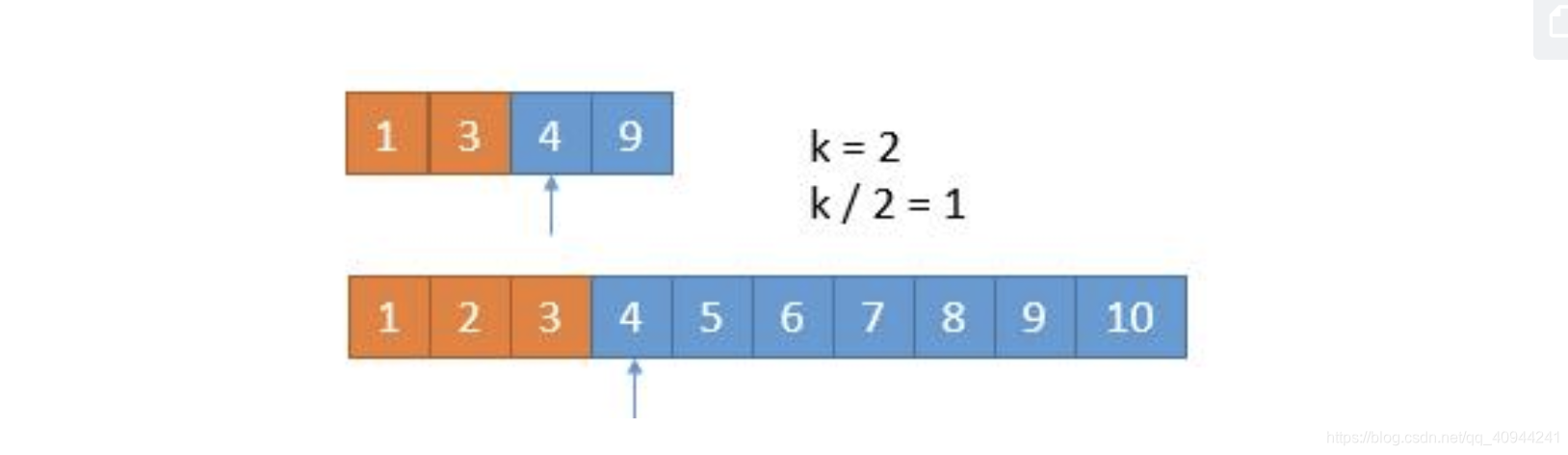

我们又排除掉 2 个数字，所以现在找第 4 - 2 = 2 小的数字就可以了。此时比较两个数组中的第 k / 2 = 1 个数，4 == 4，怎么办呢？由于两个数相等，所以我们无论去掉哪个数组中的都行，因为去掉 1 个总会保留 1 个的，所以没有影响。为了统一，我们就假设 4 > 4 吧，所以此时将下边的 4 去掉。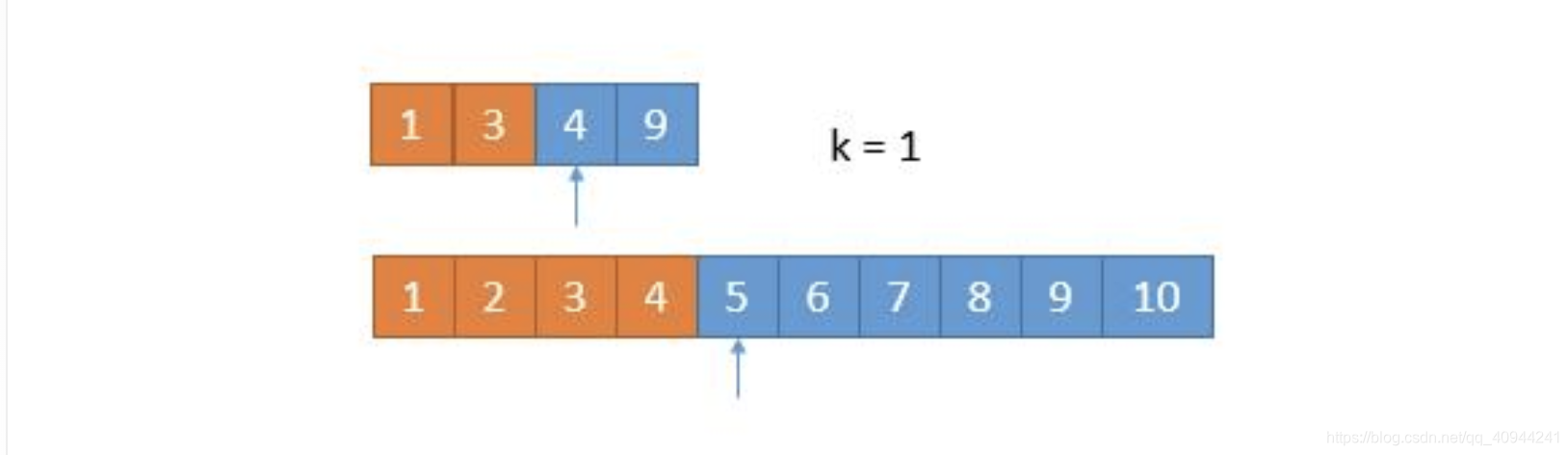

由于又去掉 1 个数字，此时我们要找第 1 小的数字，所以只需判断两个数组中第一个数字哪个小就可以了，也就是 4。

所以第 7 小的数字是 4。

我们每次都是取 k/2 的数进行比较，有时候可能会遇到数组长度小于 k/2的时候。

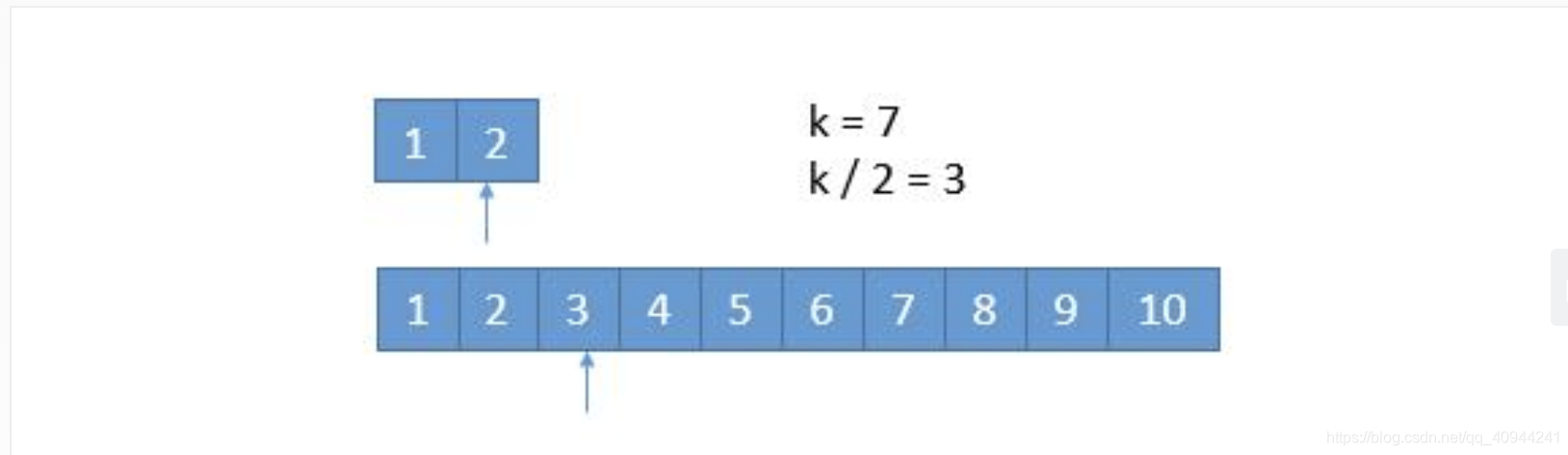
此时 k / 2 等于 3，而上边的数组长度是 2，我们此时将箭头指向它的末尾就可以了。这样的话，由于 2 < 3，所以就会导致上边的数组 1，2 都被排除。造成下边的情况。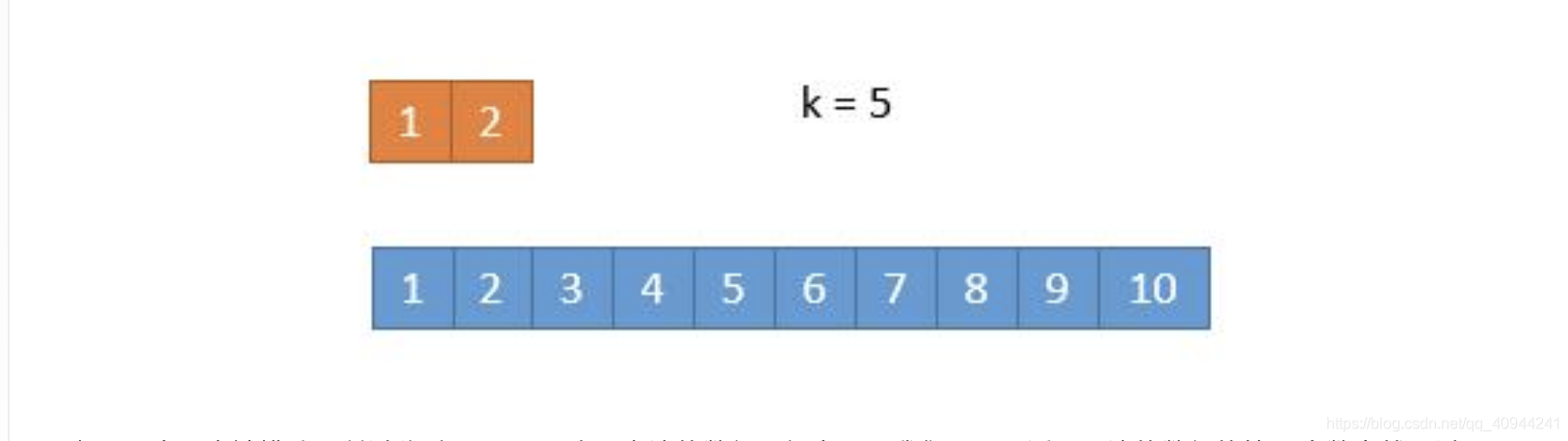

由于 2 个元素被排除，所以此时 k = 5，又由于上边的数组已经空了，我们只需要返回下边的数组的第 5 个数字就可以了。

从上边可以看到，无论是找第奇数个还是第偶数个数字，对我们的算法并没有影响，而且在算法进行中，k 的值都有可能从奇数变为偶数，最终都会变为 1 或者由于一个数组空了，直接返回结果。

所以我们采用递归的思路，为了防止数组长度小于 k/2，所以每次比较 min(k/2，len(数组) 对应的数字，把小的那个对应的数组的数字排除，将两个新数组进入递归，并且 k 要减去排除的数字的个数。递归出口就是当 k=1 或者其中一个数字长度是 0 了。

public double findMedianSortedArrays(int[] nums1, int[] nums2) {
    int n = nums1.length;
    int m = nums2.length;
    int left = (n + m + 1) / 2;
    int right = (n + m + 2) / 2;
    //将偶数和奇数的情况合并，如果是奇数，会求两次同样的 k 。
    return (getKth(nums1, 0, n - 1, nums2, 0, m - 1, left) + getKth(nums1, 0, n - 1, nums2, 0, m - 1, right)) * 0.5;  
}
    
    private int getKth(int[] nums1, int start1, int end1, int[] nums2, int start2, int end2, int k) {
        int len1 = end1 - start1 + 1;
        int len2 = end2 - start2 + 1;
        //让 len1 的长度小于 len2，这样就能保证如果有数组空了，一定是 len1 
        if (len1 > len2) return getKth(nums2, start2, end2, nums1, start1, end1, k);
        if (len1 == 0) return nums2[start2 + k - 1];

        if (k == 1) return Math.min(nums1[start1], nums2[start2]);

        int i = start1 + Math.min(len1, k / 2) - 1;
        int j = start2 + Math.min(len2, k / 2) - 1;

        if (nums1[i] > nums2[j]) {
            return getKth(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1));
        }
        else {
            return getKth(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1));
        }
    }

时间复杂度：每进行一次循环，我们就减少 k/2 个元素，所以时间复杂度是 O(log(k)，而 k=(m+n)/2，所以最终的复杂也就是 O(log(m+n）。

空间复杂度：虽然我们用到了递归，但是可以看到这个递归属于尾递归，所以编译器不需要不停地堆栈，所以空间复杂度为 O(1)。

解题思路二

我们先理一下中位数的定义是什么：

中位数（又称中值，英语：Median），[统计学] (https://baike.baidu.com/item/%E7%BB%9F%E8%AE%A1%E5%AD%A6/2630438)中的专有名词，代表一个样本、种群或 [概率分布] (https://baike.baidu.com/item/%E6%A6%82%E7%8E%87%E5%88%86%E5%B8%83/828907)中的一个数值，其可将数值集合划分为相等的上下两部分。

所以我们只需要将数组进行切分。
一个长度为m的数组有m+1个位置可以切：

我们把数组 A 和数组 B 分别在 i 和 j 进行切割。

将 i 的左边和 j 的左边组合成「左半部分」，将 i 的右边和 j 的右边组合成「右半部分」。

当数组A和数组B的总长度之和为偶数时，如果我们能够保证左半部分的长度等于右半部分，左半部分最大的值小于右半部分最小的值，那么中位数就可以表示为（左半部分最大值+右半部分最小值）/ 2，用公式的方法可以表示为：

1） i + j = m - i  + n - j  , 也就是 j = ( m + n ) / 2 - i

2） max ( A [ i - 1 ] , B [ j - 1 ]）） <= min ( A [ i ] , B [ j ]））

中位数表示为：（max ( A [ i - 1 ] , B [  j  - 1 ]）+ min ( A [ i ] , B [ j ]）） /  2

当数组A和数组B的总长度之和为奇数时，如果我们能保证左半部分的长度比右半部分多1，左半部分最大的值小于右半部分最小的值，那么中位数就是左半部分比右半部分多出的那个数。公式表示为：

1）i + j = m - i  + n - j  + 1也就是 j = ( m + n + 1) / 2 - i

2） max ( A [ i - 1 ] , B [ j - 1 ]）） <= min ( A [ i ] , B [ j ]））

中位数表示为：max ( A [ i - 1 ] , B [  j - 1 ]）

上边的第一个条件我们其实可以合并为 j = ( m + n + 1) / 2 - ij=(m+n+1)/2−i，因为如果 m + n 是偶数，由于我们取的是 int值，所以加 1 也不会影响结果。当然，由于 0 <= i <= m，为了保证 0 <= j <= n，我们必须保证 m <= n。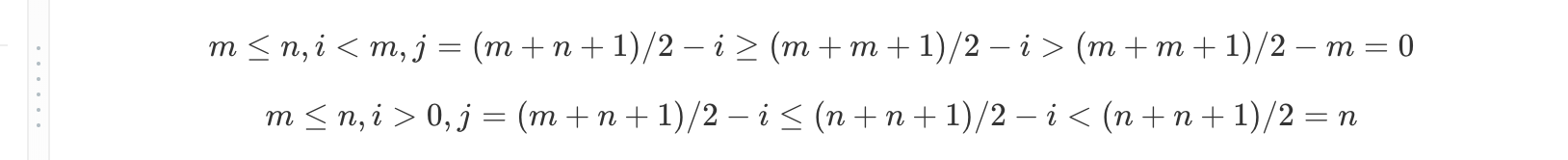

最后一步由于是 int 间的运算，所以 1/2=0。

而对于第二个条件，奇数和偶数的情况是一样的，我们进一步分析。为了保证 max ( A [ i - 1 ] , B [ j - 1 ]）） <= min ( A [ i ] , B [ j ]）），因为 A 数组和 B 数组是有序的，所以 A [ i - 1 ] <= A [ i ]，B [ i - 1 ] <= B [ i ] 这是天然的，所以我们只需要保证 B [ j - 1 ] < = A [ i ] 和 A [ i - 1 ] <= B [ j ] 所以我们分两种情况讨论：

B [ j - 1 ] > A [ i ]，并且为了不越界，要保证 j != 0，i != m：

此时很明显，我们需要增加 i ，为了数量的平衡还要减少 j ，幸运的是 j = ( m + n + 1) / 2 - i，i 增大，j 自然会减少。

A [ i - 1 ] > B [ j ] ，并且为了不越界，要保证 i != 0，j != n

此时和上边的情况相反，我们要减少 i ，增大 j 。

上边两种情况，我们把边界都排除了，需要单独讨论。

边界情况：

当 i = 0, 或者 j = 0，也就是切在了最前边。

此时左半部分当 j = 0 时，最大的值就是 A [ i - 1 ] ；当 i = 0 时最大的值就是 B [ j - 1] 。右半部分最小值和之前一样。

当 i = m 或者 j = n，也就是切在了最后边。

此时左半部分最大值和之前一样。右半部分当 j = n 时，最小值就是 A [ i ] ；当 i = m 时，最小值就是B [ j ] 。

所有的思路都理清了，最后一个问题，增加 i 的方式。当然用二分了。初始化 i 为中间的值，然后减半找中间的，减半找中间的，减半找中间的直到答案。

class Solution {
    public double findMedianSortedArrays(int[] A, int[] B) {
        int m = A.length;
        int n = B.length;
        if (m > n) { 
            return findMedianSortedArrays(B,A); // 保证 m <= n
        }
        int iMin = 0, iMax = m;
        while (iMin <= iMax) {
            int i = (iMin + iMax) / 2;
            int j = (m + n + 1) / 2 - i;
            if (j != 0 && i != m && B[j-1] > A[i]){ // i 需要增大
                iMin = i + 1; 
            }
            else if (i != 0 && j != n && A[i-1] > B[j]) { // i 需要减小
                iMax = i - 1; 
            }
            else { // 达到要求，并且将边界条件列出来单独考虑
                int maxLeft = 0;
                if (i == 0) { maxLeft = B[j-1]; }
                else if (j == 0) { maxLeft = A[i-1]; }
                else { maxLeft = Math.max(A[i-1], B[j-1]); }
                if ( (m + n) % 2 == 1 ) { return maxLeft; } // 奇数的话不需要考虑右半部分

                int minRight = 0;
                if (i == m) { minRight = B[j]; }
                else if (j == n) { minRight = A[i]; }
                else { minRight = Math.min(B[j], A[i]); }

                return (maxLeft + minRight) / 2.0; //如果是偶数的话返回结果
            }
        }
        return 0.0;
    }
}

思路一参考链接：https://leetcode-cn.com/problems/median-of-two-sorted-arrays/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-w-2/
思路二参考链接：https://leetcode-cn.com/problems/median-of-two-sorted-arrays/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-w-2/