分支界限法

简单概述

分支界限法类似与回溯法，也是在问题解空间中搜索问题解的一种算法。
分支界限法与回溯法对比：
1. 求解目标不同：回溯法可以用于求解目标是找出解空间树中满足约束条件的所有解，而分支界限法求解的目标通常是找出一个满足约束条件的解，或者最优解。
2. 搜索方式不同：回溯法主要以深度优先的方式搜索解空间树，而分支界限法则主要以广度优先或者函数优先的方式搜索解空间树。

基本思想

在分支界限法中，每个活结点只有一次机会成为扩展节点，一旦成为扩展结点，就一次性产生其所有儿子结点。在这些儿子结点中，导致不可行解或者导致非最优解的儿子结点被舍弃，其余儿子结点被加入活结点中。
此后，从活结点表中取下一结点成为当前扩展结点，并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活节点列表为空时为止。
代码框架：

Q = {q0};//存储所有的活结点,初始化为根节点
void Branch&Bound ()
{
	while (Q!=) {
		select a node q from Q;//从Q选择一个结点
		Branch(q, Q1); //对q进行分支，产生Q1，分支时利用约束和界进行剪枝
		add (Q1, Q);// 将新产生的活结点加入Q
        }
}

常见的两种分支搜索法

队列式(FIFO)搜索法：按照队列先进先出（FIFO）原则选取下一个节点为扩展节点。

优先队列式搜索法：按照优先队列中规定的优先级选取优先级最高的节点成为当前扩展节点。

最大堆（最大优先队列）：最大效益优先
最小堆（最小优先队列）：最小耗费优先

经典问题案例

01背包问题

问题描述

有n 种不同的物品，每个物品有两个属性，size 体积，value 价值，现在给一个容量为 w 的背包，问最多可带走多少价值的物品。

例：编号分别为a,b,c,d,e的五件物品，它们的重量分别是2,2,6,5,4，它们的价值分别是6,3,5,4,6，每件物品数量只有一个，现在给你个承重为10的背包，如何让背包里装入的物品具有最大的价值总和？

解题思路

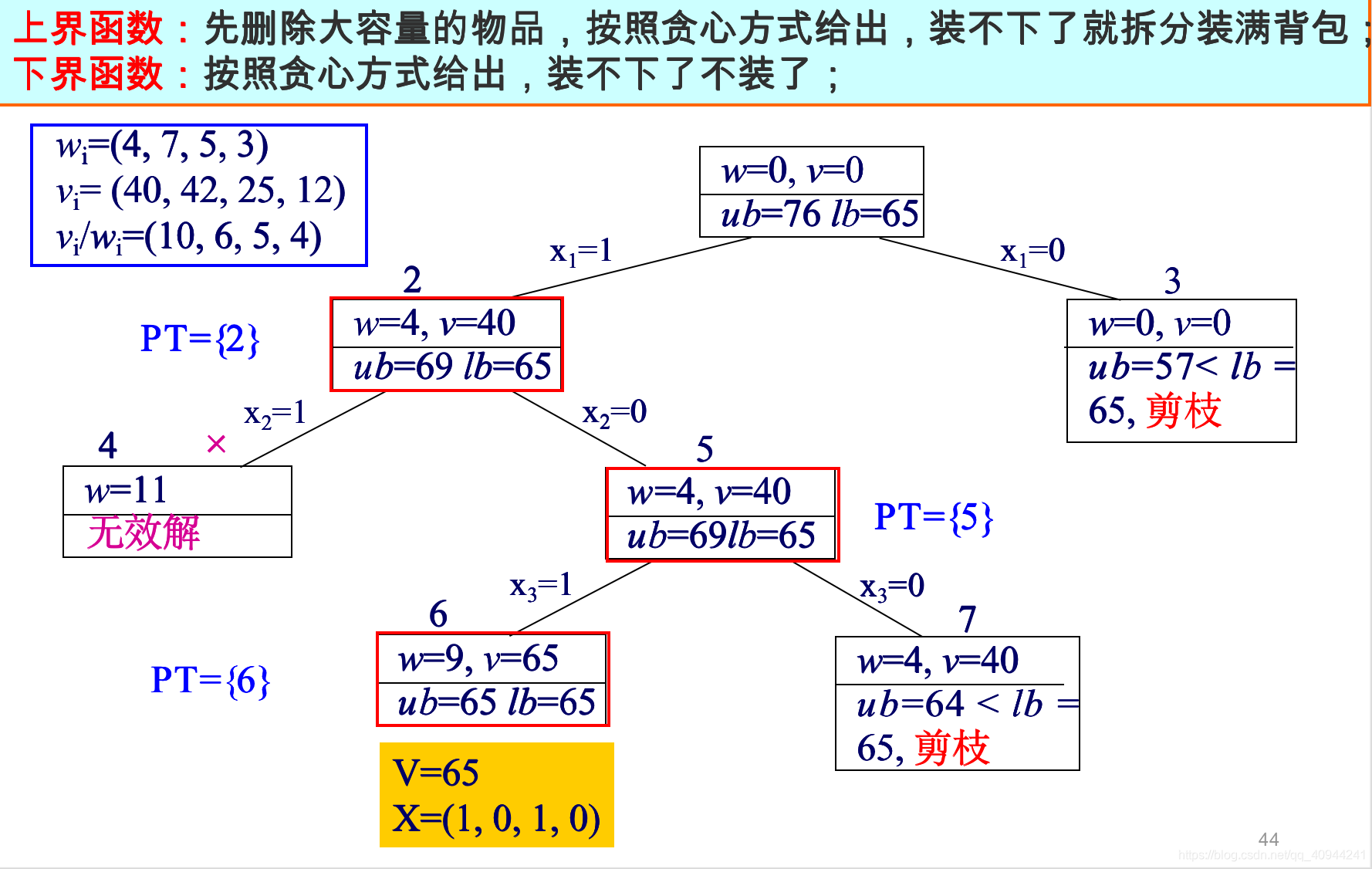
问题的关键在于解空间树的界的设计，好的界限函数可以大大提高算法的效率。01背包问题是求解在限定条件下的极大值，所以上界函数的设计很重要，因为我们可以根据计算出来的上界值和之前算出的下界做比较，如果当前的上界比下界还要小，那么就可以剪枝，减少计算量。
01背包问题的上界函数可以使用这种方法，我们先删除比背包剩余容量还要大的物品（因为不可能放得下），然后按照贪心算法的方式：分别计算出每个物品的价值比（价值/重量），价值比大的就先装。因为是计算上界，我们不用考虑装不下的问题，如果装不下，就拆分，按照比例装入背包。下界函数的设计和上界函数的思路差不多，但是由于是下界，所以我们要考虑装不下的情况，如果装不下，那就不装，换成下一个价值比大的物品继续装。
构造解空间树的过程如下：

代码实现

package branch;

import java.util.*;

public class Package01 {

    private int maxValue = Integer.MIN_VALUE;
    private static   LinkedList<Node> heap = new LinkedList<Node>();//创建一个指针链表

    public int getMaxValue() {
        return maxValue;
    }

    public void setMaxValue(int maxValue) {
        this.maxValue = maxValue;
    }

    public static class Node implements Comparable{
        double ub; //价值上界
        int lb; //价值下界
        int level; //所在层数
        Node parent; //父节点
        int cValue; //当前价值
        int restPWeight; //剩余背包容量
        public Node(double ub,int lb,int level,Node node,int cValue,int restPWeight){
            this.ub = ub;
            this.lb = lb;
            this.level = level;
            this.parent = node;
            this.cValue = cValue;
            this.restPWeight = restPWeight;
        }

        @Override
        public int compareTo(Object o) {
            double compareUb = ((Node)o).ub;
            if(ub < compareUb) return 1;
            if(ub == compareUb) return 0;
            return -1;
        }
        public boolean equals(Object x){
            return ub==((Node)x).ub;
        }
    }


        /**
     * 用贪心法算出最优解的下界lb
     * @param weight 对应物品重量
     * @param value 对应物品的价值
     * @param pWeight 背包重量
     * @return 返回求出的下界
     */
    private static int computeLb(int[] weight, int[] value, int pWeight){
        int lb = 0;
        Map<Integer,Integer> omap = new HashMap<>();
        Map<Integer,Integer> map = new TreeMap<>(new Comparator<Integer>() {
            public int compare(Integer obj1, Integer obj2) {
                // 降序排序
                return obj2.compareTo(obj1);
            }
        });//按照key对map进行排序
        for(int i = 1;i <= weight.length;i++){
            omap.put((value[i-1]/weight[i-1]),i);
        }
        map.putAll(omap);
        //遍历map，得到排好序的物品编号顺序
        for(Map.Entry<Integer,Integer> entry: map.entrySet()){
            int number = entry.getValue();
            //判断物品是否能被装下
            if(weight[number - 1] > pWeight) continue;
            pWeight = pWeight - weight[number - 1];
            lb = lb + value[number - 1];
        }
        return lb;
    }

    /**
     * 用贪心法算出最优解的上界ub
     * @param weight 对应物品重量
     * @param value 对应物品的价值
     * @param pWeight 背包重量
     * @return 返回求出的上界
     */
    private static double computeUb(int[] weight,int[] value,int pWeight){
        double ub = 0;
        int cpweight = pWeight; //当前背包容量
        Map<Integer,Integer> omap = new HashMap<>();
        Map<Integer,Integer> map = new TreeMap<>(new Comparator<Integer>() {
            public int compare(Integer obj1, Integer obj2) {
                // 降序排序
                return obj2.compareTo(obj1);
            }
        });//按照key对map进行排序
        for(int i = 1;i <= weight.length;i++){
            omap.put((value[i-1]/weight[i-1]),i);
        }
        map.putAll(omap);
//        System.out.println(map);
        //遍历map，得到排好序的物品编号顺序
        for(Map.Entry<Integer,Integer> entry: map.entrySet()){
            int number = entry.getValue();
            if(weight[number - 1] > pWeight)continue;
            if(weight[number - 1] > cpweight){
                ub = ub + cpweight * entry.getKey();
                return ub;
            }else {
                cpweight = cpweight - weight[number - 1];
                ub = ub + value[number - 1];
            }
        }
        return ub;
    }

    public static void main(String[] args) {
    	//代码的排序过程待优化
        int[] weight = {4,7,5,3,2,1}; //物品重量
        int[] value = {40,42,25,12,6,2}; //物品价值
        int maxLevel = weight.length;
        int pWeight = 10; //背包重量
        int[] result = new int[maxLevel]; //用来存储结果
        int maxValue = 0; //存储方案最大价值
        int lb = computeLb(weight,value,pWeight);//计算出下界
        double ub = computeUb(weight,value,pWeight);//计算出上界
        System.out.println(lb+" "+ub);
        int level = 1;
        Node node = new Node(ub,lb,level,null,0,pWeight);
        //搜索子集空间树
        while (node!=null&&node.level<=maxLevel){
          //参考优先队列，不停的扩展结点，选取下一个结点
                //选择装入
            if(node.restPWeight-weight[node.level - 1] >= 0) {
                int[] cweight = Arrays.copyOfRange(weight, node.level, maxLevel);//去掉已经判断过的物品，下面同理
                int[] cvalue = Arrays.copyOfRange(value, node.level, maxLevel);
                double nodeub = node.cValue + value[node.level - 1] + computeUb(cweight, cvalue, node.restPWeight - weight[node.level - 1]); //算出当前上界
                int nodelb = lb; //当前下界
                int nodevalue = value[node.level - 1];//当前判断是否装入物品的价值
                if (nodeub >= lb) {
                    //创建节点
                    Node childNode = new Node(nodeub, nodelb, node.level + 1, node, node.cValue + nodevalue, node.restPWeight - weight[node.level - 1]);
                    heap.add(childNode);
                    int cValue = node.cValue+value[node.level-1];
                    if(cValue > maxValue) maxValue = cValue;
                    result[node.level - 1] = 1;
                    Collections.sort(heap);
                }
            }
                //选择不装入
                int[] cweight1 = Arrays.copyOfRange(weight,node.level,maxLevel);//去掉已经判断过的物品，下面同理
                int[] cvalue1 = Arrays.copyOfRange(value,node.level,maxLevel);
                double nodeub1 = node.cValue+computeUb(cweight1,cvalue1,node.restPWeight); //算出当前上界
                int nodelb1 = lb; //当前下界
                if(nodeub1>=lb){
                    //创建节点
                    Node childNode1 = new Node(nodeub1,nodelb1,node.level+1,node,node.cValue,node.restPWeight);
                    heap.add(childNode1);
                    int cValue = node.cValue;
                    if(cValue > maxValue) maxValue = cValue;
                    Collections.sort(heap);
                }
            node = heap.poll();
        }
        System.out.println(maxValue);
        for(int i = 0;i<result.length;i++){
            System.out.print(result[i]+" ");
        }
    }
}

最大团问题

问题概述

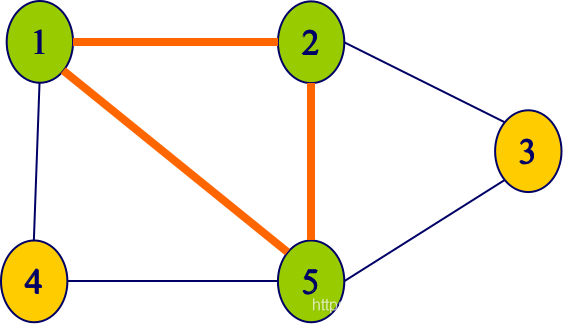
举个例子：下图G中，子集{1,2}是G的大小为2的完全子图。这个完全子图不是团，因为它被G更大的完全子图{1,2,5}包含。{1,2,5}是G的最大团。{1,4,5}和{2,3,5}也是G的最大团。

解题思路

我们用分支界限法解决问题时，首先要构建问题的解空间数，从题意不难看出，问题是一个子集树，对于每个顶点，都有选或不选两种情况，所以是子集树，然后是上界函数和下界函数。这个问题的下界函数不容易求解，我们可以直接把当前最优解当作下界函数。

上界函数：用变量cliqueSize表示与该结点相应的团的顶点数；level表示结点在子集空间树中所处的层次；用cliqueSize+n-level+1作为顶点数上界upperSize的值。
在此优先队列式分支限界法中，upperSize实际上也是优先队列中元素的优先级。算法总是从活结点优先队列中抽取具有最大upperSize值的元素作为下一个扩展元素。

算法思想：
子集树的根结点是初始扩展结点，对于这个特殊的扩展结点，其cliqueSize的值为0。算法在扩展内部结点时，首先考察其左儿子结点。在左儿子结点处，将顶点i加入到当前团中，并检查该顶点与当前团中其他顶点之间是否有边相连。当顶点i与当前团中所有顶点之间都有边相连，则相应的左儿子结点是可行结点，将它加入到子集树中并插入活结点优先队列，并判断是否可以更新最优解，否则就不是可行结点。

接着继续考察当前扩展结点的右儿子结点。当upperSize > bestn时，右子树中可能含有最优解，此时将右儿子结点加入到子集树中并插入到活结点优先队列中。不断从优先队列中选取活节点，并按照上面的方式（先左子树，后右子树）扩展节点，直到满足终止条件。

终止条件：
算法的while循环的终止条件是遇到子集树中的一个叶结点(即n+1层结点)成为当前扩展结点。
对于子集树中的叶结点，有upperSize＝cliqueSize。此时活结点优先队列中剩余结点的upperSize值均不超过当前扩展结点的upperSize值，从而进一步搜索不可能得到更大的团，此时算法已找到一个最优解。

代码实现

package branch;


import java.util.Collections;
import java.util.LinkedList;
import java.util.Vector;

import static java.lang.Integer.max;

/**
 * Created by zhangyun on 2019/12/17
 * 最大团问题
 */
public class MaxClique {

    private LinkedList<Node> heap = new LinkedList<Node>();//创建一个指针链表

    /**
     * 树节点的结构体
     */
    public  class Node implements Comparable{
        double cliqueSize; //价值上界
        int level; //所在层数
        Vector<Integer> selectedNode = new Vector<>(); //存储已选节点
        public Node(double cliqueSize,int level,Vector<Integer> nodes){
            this.selectedNode.addAll(nodes);
            this.cliqueSize = cliqueSize;
            this.level = level;
        }

        /**
         * 重写比较器，ub大的先出栈
         */
        @Override
        public int compareTo(Object o) {
            double compareUb = ((Node)o).cliqueSize;
            if(cliqueSize< compareUb) return 1;
            if(cliqueSize == compareUb) return 0;
            return -1;
        }
        public boolean equals(Object x){
            return cliqueSize==((Node)x).cliqueSize;
        }
    }

    /**
     *
     * @param nodeIndex 每个节点的与其他节点是否有边，有边为1，无边为0,根节点全部初始化为0
     * @param n 节点总数
     * @return
     */
    public int maxClique(int[][] nodeIndex,int n){
        int bestNum = 0; //最优解
        int cliqueSize = 0; //cliqueSize = cliqueSize + n - level + 1顶点数上界upperSize的值
        int level = 0; //层级从0开始，此时团内无节点
        int upperSize = cliqueSize + n - level; // 上界
        Vector<Integer> selectedNode = new Vector<>();
//        int[] nodes = new int[n + 1]; //存储顶点
//        //写入顶点{0,1,2,3,...,n},0表示根节点，实际不存在,为了使节点与level对应
//        for(int i = 0;i <= n;i++){
//            nodes[i] = i ;
//        }
        Node node = new Node(cliqueSize,level,selectedNode); //初始化根节点，下标为0
        while(node.level < n - 1){
            if(node.level + 1 == n - 1) return node.selectedNode.size();
            //扩展左子树
            if(ifEdge(nodeIndex,node.level + 1,node.selectedNode)){
                Vector<Integer> childSelectedNode = new Vector<>();
                childSelectedNode.addAll(node.selectedNode);
                childSelectedNode.add(level + 1);
                int upper = node.selectedNode.size() + n - node.level; //计算上界
                Node leftChild = new Node(upper,node.level + 1,childSelectedNode);
                heap.add(leftChild);
                Collections.sort(heap);
            }
            //扩展右子树,因为不加节点，不用判断是否右边，但是要比较上界和最优解的大小
            //如果当前上界大于最优解的话，说明可能有最优解在子树中，加入队列
            if(node.selectedNode.size() + n - node.level >= bestNum){
                Vector<Integer> childSelectedNode = new Vector<>();
                childSelectedNode.addAll(node.selectedNode);
                int upper = node.selectedNode.size() + n - node.level - 1; //计算上界
                Node rightChild = new Node(upper,node.level + 1, childSelectedNode);
                heap.add(rightChild);
                Collections.sort(heap);
            }
            node = heap.poll();
            bestNum = max(bestNum,node.selectedNode.size()); // 加入节点后更新最优解
        }
        return 0;
    }

    /**
     * 判断要加入节点和其他节点是否右边
     * @param nodeIndex 每个节点的与其他节点是否有边，有边为1，无边为0，根节点全部初始化为0
     * @param level 要加入节点的层级
     * @param selectedNode 已加入节点的层级
     * @return
     */
    public boolean ifEdge(int[][] nodeIndex,int level,Vector<Integer> selectedNode){
        for(int i = 0;i < selectedNode.size();i++){
            if(nodeIndex[selectedNode.get(i)][level] == 0)
                return false;
        }
        return true;
    }
}

测试类：

public class TestMaxClique {
    public static void main(String[] args) {
        int[][] nodes = {{0,0,0,0,0,0},
                         {0,0,1,0,1,1},
                         {0,1,0,1,0,1},
                         {0,0,1,0,0,1},
                         {0,1,0,0,0,1},
                         {0,1,1,1,1,0}};
        int n = nodes.length;
        MaxClique maxClique = new MaxClique();
        int num = maxClique.maxClique(nodes,n);
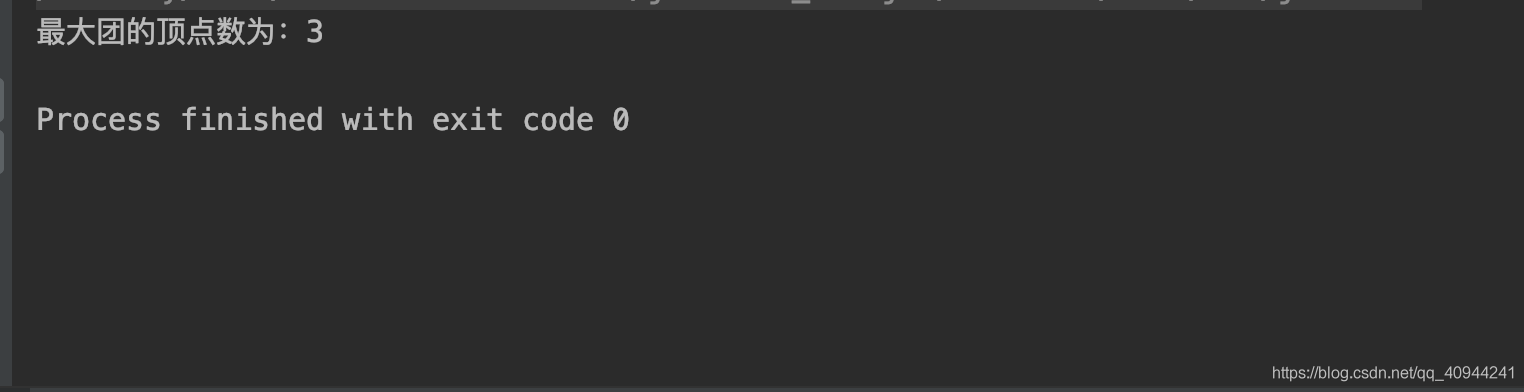
        System.out.println("最大团的顶点数为：" + num);
    }
}

测试结果：